Intermediate : Bridge Flutter
*KEYWORD *TITLE *DATABASE_BINARY_D3PLOT *DEFINE_CURVE_TITLE
*ICFD_BOUNDARY_FSI *ICFD_BOUNDARY_NONSLIP *ICFD_BOUNDARY_PRESCRIBED_VEL *ICFD_BOUNDARY_PRESCRIBED_PRE *ICFD_CONTROL_OUTPUT
*ICFD_CONTROL_FSI *ICFD_CONTROL_TIME *ICFD_MAT *ICFD_PART *ICFD_PART_VOL *ICFD_SECTION *INCLUDE *MESH_BL *MESH_SURFACE_ELEMENT *MESH_SURFACE_NODE *MESH_VOLUME *PARAMETER *END
*KEYWORD
*include
mesh_struc.k
*CONTROL_IMPLICIT_DYNAMICS
$# imass gamma beta tdybir tdydth tdybur irate
1 0.55263 0.27701
$1,0.6,0.4
$$$$$$$$$$$$$$$$$$$$$$$$$$$
$ SOLID $
$$$$$$$$$$$$$$$$$$$$$$$$$$$
$ IMPLICIT
*CONTROL_IMPLICIT_GENERAL
$# imflag dt0 imform nsbs igs cnstn form zero_v
1 0.500000 2 0 2 0 0 0
*CONTROL_IMPLICIT_SOLUTION
$# nsolvr ilimit maxref dctol ectol rctol lstol abstol
12 200 200,1.e-6,1.e-5
*CONTROL_TERMINATION
$ endtim endcyc dtmin endeng endmas
$# endtim endcyc dtmin endeng endmas
800.00000 0 0.000 0.000 0.000
*part_inertia
1,1,1
,,,3000,,802
$0.4438E+03,0.0,0.0,0.5329E+05,0.0,25300
100,0.0,0.0,100,0.0,25300
*SECTION_SHELL
$# secid elform shrf nip propt qr/irid icomp setyp
1 12 0.000 0 1 0 0 1
$# t1 t2 t3 t4 nloc marea idof edgset
0.000 0.000 0.000 0.000 0.000 0.000 0.000 0
*MAT_RIGID
$# mid ro e pr n couple m alias
1 0617.2900 20000.000 0.400000 0.000 0.000 0.000
$# cmo con1 con2
1.000000 6 4
$# lco or a1 a2 a3 v1 v2 v3
0.000 0.000 0.000 0.000 0.000 0.000
*define_sd_orientation
1,0,0.,0.,1.
*PART
$# title
spring
$# pid secid mid eosid hgid grav adpopt tmid
2 02 02 0 0 0 0 0
*PART
$# title
spring
$# pid secid mid eosid hgid grav adpopt tmid
12 12 12 0 0 0 0 0
$*PART
$# title
$damper
$# pid secid mid eosid hgid grav adpopt tmid
$ 3 3 3 0 0 0 0 0
*SECTION_DISCRETE
$# secid dro kd v0 cl fd
2 1 0.000 0.000 0.000 0.000
$# cdl tdl
0.000 0.000
*SECTION_DISCRETE
$# secid dro kd v0 cl fd
12 0 0.000 0.000 0.000 0.000
$# cdl tdl
0.000 0.000
*MAT_LINEAR_ELASTIC_DISCRETE_BEAM
$# mid ro tkr tks tkt rkr rks rkt
20 0.010000 0 0.000 0.000 0.000 0.000 61.685
$# tdr tds tdt rdr rds rdt
0.000 0.000 0.000 0.000 0.000 0
$# for fos fot mor mos mot
0 0.000 0.000 0.000 0.000 0.000
$ 0 0.000 0.000 0.000 0.000 0.000
*SECTION_BEAM
$# secid elform shrf qr/irid cst scoor nsm
20 6 1.000000 2 0 0.000 0.000
$# vol iner cid ca offset rrcon srcon trcon
1.000000 0.000 0 0.000 0.000 0.000 0.000 0.000
*MAT_SPRING_ELASTIC
$# mid k
2 40000
*MAT_SPRING_ELASTIC
$# mid k
12 2000
*SECTION_DISCRETE
$# secid dro kd v0 cl fd
3 1 0.000 0.000 0.000 0.000
$# cdl tdl
0.000 0.000
*MAT_DAMPER_VISCOUS
$# mid dc
3 78.540000
$1
*DEFINE_CURVE
$# lcid sidr sfa sfo offa offo dattyp
10 0 0.000 0.000 0.000 0.000 0
$# a1 o1
0.000 0.000
0.100000 9.810000
1000.000000 9.810000
*END
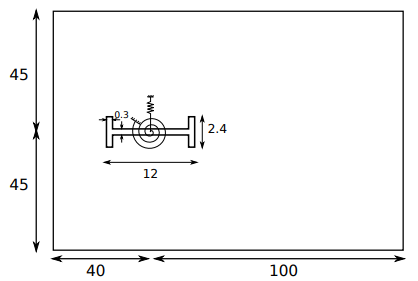
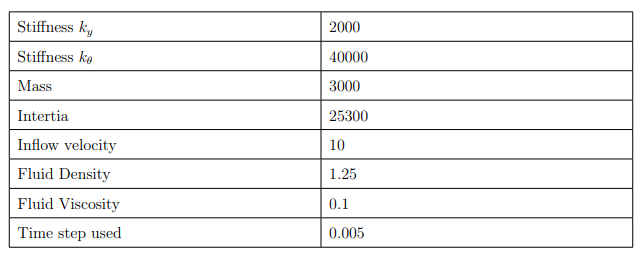
In this example, a rigid H profile bridge is considered based on the model by [2] and used in [1] . It is supported with a rotational and a vertical translation linear elastic spring. The horizontal motion is fixed to zero. The rigid body is exposed to uniform fluid flow in the horizontal direction. Bridge oscillations may consequently occur due to vertical or rotational galloping. Coupled galloping of two or more degrees of freedom is commonly known as flutter [1].
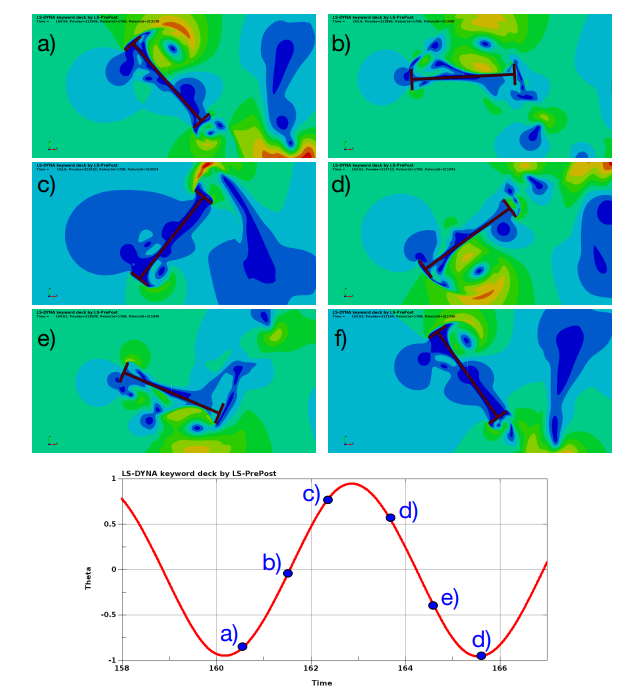
It appears clearly that the rotation is the dominant motion with severe oscillations. This is further confirmed by the rotational and translation frequencies which coincide at f0 = 0.183s which is close to the natural rotational frequency fθ = 0.200s and fy = 0.13s. The amplitude of the rotations is max(θ) = 57◦ and the maximum vertical displacement is obtained as 0.72 ≤ max(Y ) ≤ 0.84 which is again is very good agreement with the results by [1].
References :
[1] W. Dettmer and D. Peric, A computational framework for fluid-rigid body interaction: Finite element formulation and applications, Computer methods in applied mechanics and engineering, 195 (2006), pp. 1633–1666.
[2] B. Hubner, E. Walhorn, and D. Dinkler, Strongly coupled analysis of fluid structure interaction using space-time finite elements, ECCM, 2001.